1 場合の数って何?
「場合の数」って、小学校6年生で習うちょっとややこしい単元ですよね。でも簡単に言えば、「考えられるすべてのパターンの数」のことです。この数が、確率を計算するときの分母になります。

例えば、10本のくじがあって、そのうち2本が当たりだとします。この場合、当たる確率は「10分の2」ですが、場合の数は「10通り」です。確率までは小学校で習いませんが、この場合の数をしっかり理解することがポイントになります。
場合の数を求める方法は主に2つあります。
【順列】
「順番を考える」場合の数の出し方です。
例:数字「1」「2」「3」を1列に並べたときの3桁の数は何通り?
- 百の位にくる数字は3種類。
- 1つの数が決まると、残りは2種類なので十の位は2種類。
- 最後の一の位は自動的に1種類。
これらを掛け算すると、3 ×2 ×1 = 6通りになります。
【組み合わせ】
「順番を考えない」場合の数の出し方です。
例:A、B、Cの3チームで総当たり戦をすると試合数は何試合?
- 1チーム目は3種類、2チーム目は2種類で、3 ×2 = 6通り。
でも、A対BとB対Aは同じ試合なので、重複分を除いて、6 ÷ 2 = 3試合となります。
2 場合の数の求め方、他にもあります!
「順列」や「組み合わせ」で公式のように計算する方法もありますが、小学生には少し難しいですよね。そこでおすすめなのが、次のような地道な方法です。
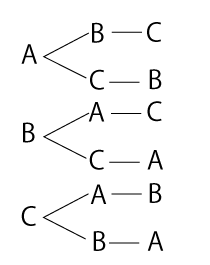
【樹形図】
数字やアルファベットを、木の枝が分かれるように順番に書き出していく方法です。これなら「抜け」や「だぶり」を防ぎやすいですよね。
【書き出し】
3桁の数字や試合のパターンを1つ1つ書き出して確認する方法です。確かに手間はかかりますが、最終的にはミスを防げるので根性勝負も必要な学びです!
ちなみに、中学生の問題でもどうしても公式では解けず、「しらみつぶし」に解くしかないことがあります。そういうとき、地道な作業を経験しておくと意外と役立つものです!
場合の数の理解は、算数だけでなく、中学・高校の数学、そして日常生活の「考え方」にもつながります。ちょっとずつ練習して慣れることが大切ですね!